Fractales en Caml

Pour les incultes : Caml qu’est-ce que c’est ?
Caml est un langage de programmation développé par l’INRIA (Institut National de la Recherche en Informatique et Automatique) au cours des années 90, et c’est surtout le langage qu’on apprend en option informatique en prépa MP. Il existe deux « branches » de Caml : Caml Light (celui qu’on utilise en prépa) et Objective Caml (encore développé actuellement).

Pour ceux qui auraient un peu de temps à perdre, vous pouvez télécharger Caml à cette adresse : http://caml.inria.fr. Pour les fractales, il faut au moins en avoir vu une fois dans sa vie, et les deux que j’ai programmé en Caml sont certainement les deux plus connues : les ensembles de Mandelbrot et Julia.

Sommaire :

Fractales :
– Ensemble de Mandelbrot
– Ensemble de Julia
– Triangle de Sierpinski
– Tapis de Sierpinski

Autres :
– Le Yin et le Yang

Fractales :

– Ensemble de Mandelbrot

 

Présentation :

De toutes les fractales, celle-ci est certainement la plus connue. L’ensemble de Mandelbrot est l’ensemble des points du plan (représentés par le nombre complexe z = x + iy) pour lesquels la suite zn+1 = zn² + z avec z0 = 0 converge (en module).

Il doit son nom au mathématicien français Benoît Mandelbrot qui l’étudia en 1979. L’ensemble est ici représenté en bleu (en fait, ce n’est pas l’ensemble lui-même qui est représenté mais une approximation de l’ensemble car on limite le nombre d’itérations). Les zones entre bleu et noir indiquent une divergence plus ou moins rapide (plus c’est foncé, plus la suite diverge rapidement). J’ai représenté ici la fractale en bleu sur fond noir. Vous pouvez changer les couleurs en modifiant le programme, mais bon c’est joli le bleu 🙂

Résultat :

Ensemble de Mandelbrot

Ensemble de Mandelbrot

Programme :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#open "graphics";;
open_graph "";;
clear_graph ();;
 
let diverge_mandelbrot a b n =
let x = ref a in
let y = ref b in
let xtemp=ref 0. in
let ytemp=ref 0. in
let k = ref 0 in
 
while ((!x *. !x+. !y *. !y) < 4.) && (!k < n) do
xtemp:=(!x)*. (!x)-. (!y)*. (!y)+. a;
ytemp:=2. *. (!x) *.(!y)+. b;
x:= !xtemp;
y:= !ytemp;
k:= !k+1;
done;
(!k);;
 
let mandelbrot n d =
clear_graph ();
let k = ref 0 in
for x=(-511) to (511) do
for y=(-383) to (383) do
k:=((diverge_mandelbrot ((float_of_int x) /. d) ((float_of_int y) /. d) n)*10);
set_color (rgb (0) ((!k)/2) (!k));
plot (512+x) (384+y);
done;
done;;
 
mandelbrot 20 200.;;
(* le premier nombre en argument correspond au nombre d'itérations et le deuxième à un coefficient de zoom *)
(* le premier nombre est de type int mais le deuxième de type float *)

– Ensemble de Julia

 

Présentation :

L’ensemble de Julia lié au paramètre c est l’ensemble des points du plan (représentés par le nombre complexe z = x + iy) pour lesquels la suite zn+1 = zn² + c avec z0 = 0 converge (en module) avec c un paramètre complexe. Les ensembles de Julia doivent leur nom au mathématicien français Gaston Julia.

La différence avec l’ensemble de Mandelbrot est que le c est le même pour tous les points du plan (alors que pour Mandelbrot la suite était zn+1 = zn² + z). L’ensemble de Mandelbrot est ainsi l’ensemble des points C d’affixe c du plan tel que l’ensemble de Julia avec pour paramètre c correspondant est connexe.

Vous pouvez modifier le programme de manière à changer les couleurs.
Quelques valeurs de c qui donnent de jolis résultats :
c = -0.181 – 0.667 i (celle que j’utilise)
c =sqrt(2.)/.2. i
c =-0.7927 + 0.1609 i
c =0.32 + 0.043 i
c =-0.3380 – 0.6230 i

Résultat :

Ensemble de Julia

Ensemble de Julia

Programme :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#open "graphics";;
open_graph "";;
clear_graph ();;
 
let diverge_julia a b cr ci n =
let x = ref a in
let y = ref b in
let xtemp=ref 0. in
let ytemp=ref 0. in
let k = ref 0 in
while ((!x *. !x+. !y *. !y) < 4.)&&(!k<n) do
xtemp:=(!x)*. (!x)-. (!y)*. (!y)+. cr;
ytemp:=2. *. (!x) *.(!y)+. ci;
x:= !xtemp;
y:= !ytemp;
k:= !k+1;
done;
(!k);;
 
let julia cr ci n d =
clear_graph ();
let k = ref 0 in
for x=(-511) to (511) do
for y=(-383) to (383) do
k:=((diverge_julia ((float_of_int x) /. d) ((float_of_int y) /. d) cr ci n)*10);
set_color (rgb (255-(!k)/2) (255-(!k)/2) (255-(!k)));
plot (512+x) (384+y);
done;
done;;
 
julia (-0.181) (-0.667) 100 200.;;
(* les deux premiers arguments correspondent respectivement à la partie réelle et la partie imaginaire de c et ils ont le type float *)
(* le troisième argument correspond au nombre d'itérations et il a le type int*)
(* le dernier argument correspond à un coefficient de zoom *)

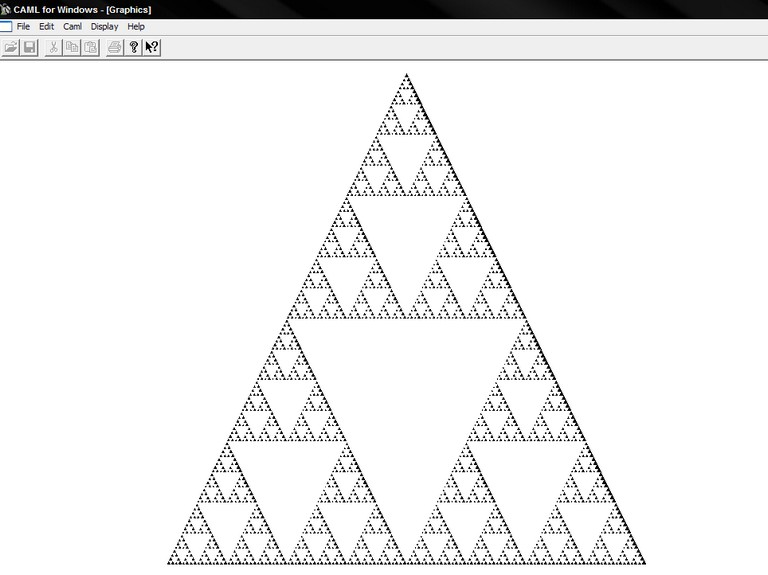
– Triangle de Sierpinski

 

Présentation :

Le principe du triangle de Sierpinski consiste à prendre un triangle, puis lui retrancher le triangle reliant les milieux de ses trois côtés, et ainsi de suite récursivement pour chaque sous-triangle.

Résultat :

Triangle de Sierpinski

Triangle de Sierpinski

Programme :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#open "graphics";;
open_graph "";;
clear_graph ();;
 
let triangle x1 y1 x2 y2 x3 y3 couleur =
set_color couleur;
fill_poly [|(x1,y1);(x2,y2);(x3,y3)|];;
 
let milieu x1 y1 x2 y2 =
((x1+x2)/2,(y1+y2)/2);;
 
let rec sierpinski_rec x1 y1 x2 y2 x3 y3 n couleur = match n with
| 0 -> ()
| _ ->
let (xm12,ym12) = milieu x1 y1 x2 y2 in
let (xm13,ym13) = milieu x1 y1 x3 y3 in
let (xm23,ym23) = milieu x2 y2 x3 y3 in
triangle xm12 ym12 xm13 ym13 xm23 ym23 couleur;
sierpinski_rec x1 y1 xm12 ym12 xm13 ym13 (n-1) couleur;
sierpinski_rec x2 y2 xm12 ym12 xm23 ym23 (n-1) couleur;
sierpinski_rec x3 y3 xm13 ym13 xm23 ym23 (n-1) couleur;;
 
let sierpinski x1 y1 x2 y2 x3 y3 n couleurnoir couleurblanc=
clear_graph();
triangle x1 y1 x2 y2 x3 y3 couleurnoir;
sierpinski_rec x1 y1 x2 y2 x3 y3 n couleurblanc;;
 
sierpinski 212 84 812 84 512 700 7 black white;;
(* les six premiers arguments (x1 y1 x2 y2 x3 y3) correspondent aux coordonnées des 3 points du grand triangle*)
(* le septième argument correspond au nombre d'itérations - si on veut y voir quelque chose, il est recommandé de ne pas dépasser 10 *)
(* le huitième argument correspond à la couleur initiale du triangle et le neuvième à celle des triangles itérés *)

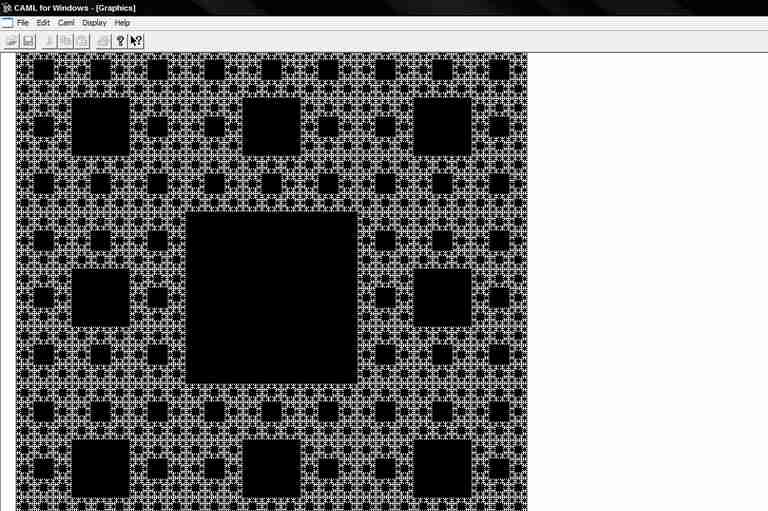
– Tapis de Sierpinski

 

Présentation :

Le principe du tapis de Sierpinski reprend celui du triangle, mais avec un carré (vous vous attendiez à quoi d’autre comme présentation ?)
Un dessin vaut mieux qu’un long discours…

Résultat :

Tapis de Sierpinski

Tapis de Sierpinski

Programme :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#open "graphics";;
open_graph "";;
clear_graph ();;
 
let carre x1 y1 x2 y2 x3 y3 x4 y4 couleur =
set_color couleur;
fill_poly [|(x1,y1);(x2,y2);(x3,y3);(x4,y4)|];;
 
let tiers x1 x2 =
((abs (x2-x1))/3);;
 
let rec tapis_rec x1 y1 x2 y2 x3 y3 x4 y4 n couleurblanc = match n with
| 0 -> ()
| _ ->
let d = ((abs (y2-y1))/3) in
 
carre (x1+d) (y1-d) (x2+d) (y2+d) (x3-d) (y3+d) (x4-d) (y4-d) couleurblanc;
tapis_rec x1 y1 x1 (y1-d) (x1+d) (y1-d) (x1+d) y1 (n-1) couleurblanc;
tapis_rec x1 (y1-d) x1 (y1-2*d) (x1+d) (y1-2*d) (x1+d) (y1-d) (n-1) couleurblanc;
tapis_rec x1 (y1-2*d) x1 (y1-3*d) (x1+d) (y1-3*d) (x1+d) (y1-2*d) (n-1) couleurblanc;
tapis_rec (x1+d) (y1-2*d) (x1+d) (y1-3*d) (x1+2*d) (y1-3*d) (x1+2*d) (y1-2*d) (n-1) couleurblanc;
tapis_rec (x1+2*d) (y1-2*d) (x1+2*d) (y1-3*d) (x1+3*d) (y1-3*d) (x1+3*d) (y1-2*d) (n-1) couleurblanc;
tapis_rec (x1+2*d) (y1-d) (x1+2*d) (y1-2*d) (x1+3*d) (y1-2*d) (x1+3*d) (y1-d) (n-1) couleurblanc;
tapis_rec (x1+2*d) y1 (x1+2*d) (y1-d) (x1+3*d) (y1-d) (x1+3*d) y1 (n-1) couleurblanc;
tapis_rec (x1+d) y1 (x1+d) (y1-d) (x1+2*d) (y1-d) (x1+2*d) y1 (n-1) couleurblanc;;
 
let tapis_sierpinski x1 y1 x2 y2 x3 y3 x4 y4 n couleurnoir couleurblanc=
clear_graph();
carre x1 y1 x2 y2 x3 y3 x4 y4 couleurnoir;
tapis_rec x1 y1 x2 y2 x3 y3 x4 y4 n couleurblanc;;
 
tapis_sierpinski 20 749 20 20 749 20 749 749 6 white black;;
(* les huit premiers arguments correspondent aux quatre sommets du grand carré - il est recommandé que le carré ait un côté égal à un multiple de (3 puissance le nombre d'itérations) *)
(* le neuvième argument correspond au nombre d'itérations - ne dépassez pas six itérations ou on ne voit plus rien *)
(* le dixième argument correspond à la couleur initiale du grand carré - ici le blanc - et le dixième à la couleur des carrés que l'on retranche - ici le noir *)
(* ne lisez pas le code source du programme, vous risquez la crise cardiaque : c'est vraiment programmé avec les pieds mais j'ai la flemme de le refaire *)

Autres :

– Le Yin et le Yang

 

Résultat :

Yin et Yang

Yin et Yang

Programme :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

#open "graphics";;
open_graph "";;
clear_graph ();;
 
let grand_cercle_noir_bas n =
set_color black;
for x=0 to (n/2) do
for y=0 to (n/2) do
if ((x*x)+(y*y)< = (n/2)*(n/2)) then begin
plot (512+x) (384-n/2+y);
plot (512+x) (384-n/2-y);
plot (512-x) (384-n/2+y);
plot (512-x) (384-n/2-y);
end;
done;
done;;
 
let grand_cercle_blanc_haut n =
set_color white;
for x=0 to (n/2) do
for y=0 to (n/2) do
if ((x*x)+(y*y)<= (n/2)*(n/2)) then begin
plot (512+x) (384+n/2+y);
plot (512+x) (384+n/2-y);
plot (512-x) (384+n/2+y);
plot (512-x) (384+n/2-y);
end;
done;
done;;
 
let petit_cercle_noir_haut n tp =
set_color black;
for x=0 to tp do
for y=0 to tp do
if ((x*x)+(y*y)<= tp*tp) then begin
plot (512+x) (384+(n/2)+y);
plot (512+x) (384+(n/2)-y);
plot (512-x) (384+(n/2)+y);
plot (512-x) (384+(n/2)-y);
end;
done;
done;;
 
let petit_cercle_blanc_bas n tp =
set_color white;
for x=0 to tp do
for y=0 to tp do
if ((x*x)+(y*y)<= tp*tp) then begin
plot (512+x) (384-(n/2)+y);
plot (512+x) (384-(n/2)-y);
plot (512-x) (384-(n/2)+y);
plot (512-x) (384-(n/2)-y);
end;
done;
done;;
 
let appartient_cercle x y a b r =
((x-a)*(x-a)+ (y-b)*(y-b) <= r*r);; let colorie_droite n = set_color black; for x=0 to n do for y=(-n) to n do if (((appartient_cercle (x+512) (y+384) 512 384 n)=true) && ((appartient_cercle (x+512) (y+384) 512 (384-(n/2)) (n/2))=false) && ((appartient_cercle (x+512) (y+384) 512 (384+(n/2)) (n/2))=false)) then begin plot (512+x) (384+y); end; done; done;; let yinyang n tp = clear_graph (); if n>384 then failwith("Fenetre trop petite : 1024x768");
if (n mod 2 = 1) then failwith("Le rayon du grand cercle doit etre un nombre pair");
grand_cercle_blanc_haut n;
grand_cercle_noir_bas n;
petit_cercle_noir_haut n tp;
petit_cercle_blanc_bas n tp;
set_color black;
draw_circle 512 384 n;
colorie_droite n;;
 
yinyang 300 30;;
(* le premier nombre en argument correspond à la taille du dessin complet et le deuxième à la taille des petits cercles blanc et noir *)
(* en fait, ça ne servait à rien de se casser le bol à créer des fonctions pour remplir des cercles, elles existent déjà - trop tard c'est fait *)

a